Sunday, February 16, 2014

Volume formulas


1 litre = (10 cm)3 = 1000 cubic centimetres = 0.001 cubic metres,
1 cubic metre = 1000 litres.
Small amounts of liquid are often measured in millilitres, where
1 millilitre = 0.001 litres = 1 cubic centimetre.





Volume formulas

Shape Volume formula Variables
Cube a^3\; a = length of any side (or edge)
Cylinder 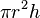\pi r^2 h\; r = radius of circular face, h = height
Prism B \cdot h B = area of the base, h = height
Rectangular prism l \cdot w \cdot h l = length, w = width, h = height
Triangular prism \frac{1}{2}bhl b = base length of triangle, h = height of triangle, l = length of prism or distance between the triangular bases
Sphere \frac{4}{3} \pi r^3 r = radius of sphere
which is the integral of the surface area of a sphere
Ellipsoid \frac{4}{3} \pi abc a, b, c = semi-axes of ellipsoid
Torus (\pi r^2)(2\pi R) = 2\pi^2 Rr^2 r = minor radius, R = major radius
Pyramid \frac{1}{3}Bh B = area of the base, h = height of pyramid
Square pyramid \frac{1}{3} s^2 h\; s = side length of base, h = height
Rectangular pyramid \frac{1}{3} lwh l = length, w = width, h = height
Cone \frac{1}{3} \pi r^2 h r = radius of circle at base, h = distance from base to tip or height
Tetrahedron[4] {\sqrt{2}\over12}a^3 \, edge length a
Parallelepiped a b c \sqrt{K}
\begin{align} K =& 1+2\cos(\alpha)\cos(\beta)\cos(\gamma) \\ & - \cos^2(\alpha)-\cos^2(\beta)-\cos^2(\gamma) \end{align} 		a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges
Any volumetric sweep
(calculus required)		 \int_a^b A(h) \,\mathrm{d}h h = any dimension of the figure,
A(h) = area of the cross-sections perpendicular to h described as a function of the position along h. a and b are the limits of integration for the volumetric sweep.
(This will work for any figure if its cross-sectional area can be determined from h).
Any rotated figure (washer method)
(calculus required)		 \pi \int_a^b \left({\left[R_O(x)\right]}^2 - {\left[R_I(x)\right]}^2\right) \mathrm{d}x R_O and R_I are functions expressing the outer and inner radii of the function, respectively.
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)